Sejarah Singkat Teorema Pythagoras

"Teorema Pythagoras" dinamakan oleh ahli matematika Yunani kuno yaitu Pythagoras, yang dianggap sebagai orang yang pertama kali memberikan bukti teorema ini. Akan tetapi, banyak orang yang percaya bahwa terdapat hubungan khusus antara sisi dari sebuah segi tiga siku-siku jauh sebelum Pythagoras menemukannya.

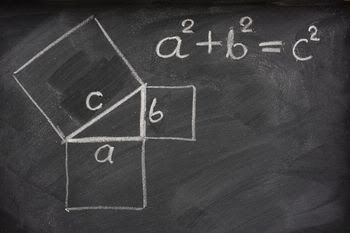
Teorema Pythagoras memainkan peran yang sangat signifikan dalam berbagai bidang yang berkaitan dengan matematika. Misalnya, untuk membentuk dasar trigonometri dan bentuk aritmatika, di mana bentuk ini menggabungkan geometri dan aljabar. Teorema ini adalah sebuah hubungan dalam Geometri Euclides di antara tiga sisi dari segi tiga siku-siku. Hal ini menyatakan bahwa 'Jumlah dari persegi yang dibentuk dari panjang dua sisi siku-sikunya akan sama dengan jumlah persegi yang dibentuk dari panjang hipotenusa-nya'.

Secara matematis, teorema ini biasanya biasanya ditulis sebagai : a2 + b2 = c2 , di mana a dan b mewakili panjang dari dua sisi lain dari segitiga siku-siku dan c mewakili panjang dari hipotenusanya (sisi miring).

Sejarah

Sejarah dari Teorema Pythagoras dapat dibagi sebagai berikut:

1. pengetahuan dari Triple Pythagoras,

2. hubungan antara sisi-sisi dari segitiga siku-siku dan sudut-sudut yang berdekatan, 3. bukti dari teorema.

Sekitar 4000 tahun yang lalu, orang Babilonia dan orang Cina telah menyadari fakta bahwa sebuah segitiga dengan panjang sisi 3, 4, dan 5 harus merupakan segitiga siku-siku. Mereka menggunakan konsep ini untuk membangun sudut siku-siku dan merancang segitiga siku-siku dengan membagi panjang tali ke dalam 12 bagian yang sama, seperti sisi pertama pada segitiga adalah 3, sisi kedua adalah 4, dan sisi ketiga adalah 5 satuan panjang.

Sekitar 2500 tahun SM, Monumen Megalithic di Mesir dan Eropa Utara terdapat susunan segitiga siku-siku dengan panjang sisi yang bulat. Bartel Leendert van der Waerden meng-hipotesis-kan bahwa Tripel Pythagoras diidentifikasi secara aljabar. Selama pemerintahan Hammurabi the Great (1790 - 1750 SM), tablet Plimpton Mesopotamian 32 terdiri dari banyak tulisan yang terkait dengan Tripel Pythagoras. Di India (Abad ke-8 sampai ke-2 sebelum masehi), terdapat Baudhayana Sulba Sutra yang terdiri dari daftar Tripel Pythagoras yaitu pernyataan dari dalil dan bukti geometris dari teorema untuk segitiga siku-siku sama kaki.

Pythagoras (569-475 SM) menggunakan metode aljabar untuk membangun Tripel Pythagoras. Menurut Sir Thomas L. Heath, tidak ada penentuan sebab dari teorema ini selama hampir lima abad setelah Pythagoras menuliskan teorema ini. Namun, penulis seperti Plutarch dan Cicero mengatributkan teorema ke Pythagoras sampai atribusi tersebut diterima dan dikenal secara luas. Pada 400 SM, Plato mendirikan sebuah metode untuk mencari Tripel Pythagoras yang baik dipadukan dengan aljabar and geometri. Sekitar 300 SM, elemen Euclid (bukti aksiomatis yang tertua) menyajikan teorema tersebut. Teks Cina Chou Pei Suan Ching yang ditulis antara 500 SM sampai 200 sesudah masehi memiliki bukti visual dari Teorema Pythagoras atau disebut dengan "Gougu Theorem" (sebagaimana diketahui di Cina) untuk segitiga berukuran 3, 4, dan 5. Selama Dinasti Han (202 SM - 220 M), Tripel Pythagoras muncul di Sembilan Bab pada Seni Mathematika seiring dengan sebutan segitiga siku-siku. Rekaman pertama menggunakan teorema berada di Cina sebagai 'theorem Gougu', dan di India dinamakan "Bhaskara theorem".

Namun, hal ini belum dikonfirmasi apakah Pythagoras adalah orang pertama yang menemukan hubungan antara sisi dari segitiga siku-siku, karena tidak ada teks yang ditulis olehnya yang ditemukan. Walaupun demikian, nama Pythagoras telah dipercaya untuk menjadi nama yang sesuai untuk teorema ini.